https://pb.ps-taiwan.org/catalog/ins.php?index_m1_id=5&index_id=560
我在學生時代就覺得熱力學第二定律很特別,因為我所學的其它物理定律都是十分嚴格以數學等式來表述,但熱力學第二定律是用不等式,好像比較不精準。本文我就熱力學第二定律及非平衡統計物理[1]近年之發展給一個簡單的回顧,同時概括描述近年來我跟多個實驗小組合作的成果。
眾所周知,熱力學第二定律中熵不減少代表的意義是“時間之箭”,指出宏觀非平衡過程中的不可逆性。但微觀的物理定律都是時間可逆的,這表面上的矛盾困擾了百多年前的科學家好一陣子,這就是著名的Loschmidt's paradox[2],其謬誤的原因主要是忽略了大部分背景粒子的自由度(如熱庫)。另一方面,隨著系統和裝置的微細化和實驗能測量的尺度更趨微奈米,我們不得不重新考慮宏觀平衡態描述漲落的原理,而進入近代非平衡統計物理的範疇。熱平衡系統的漲落的理論框架由Maxwell、Boltzmann和Gibbs開創了先河;線性響應理論(Linear Response Theory)則將此框架擴展到離熱平衡不遠處。確實,傳統上所說的很多非平衡統計物理--Onsager的對等關係 (reciprocal relations),格林-久保關係 (Green-Kubo relation)連結傳輸係數與相關函數等等,其實都是接近平衡態的統計力學。
用於理解非平衡行為的理論架構尚未達到如平衡統計物理學的簡單性和強大弁遄C但近20多年來已有突破性的理論和實驗進展。熱力學第二定律中,限制系統的熵永遠不會減少必須依賴於足夠的統計數據。由於大多數宏觀系統包含1023以上的自由度,所以宏觀系統都會滿足第二定律。但是在較小的系統中,標準的平衡物理不再足夠用來描述系統的狀態:反而統計漲落主宰著系統的物理定律。近20多年來,學界已經意識到遠離熱平衡的系統滿足一些嚴格和出乎意料的結果-稱之為漲落定理(Fluctuation Theorems, FT)。在實驗上更容易於小型系統中直接觀察到。因此漲落定理成為上世紀末最重要的物理突破發展之一[1]。其後20多年有更多新的重大進展,顯示這些非平衡漲落符合嶄新的定律。漲落定理可以表示為熵產生(entropy production, ΔS)要滿足的定律,或作為�(W)和自由能差(ΔF)之間的關係。無論哪種情況,它們都可以被視為熱力學第二定律的精確延伸,取代 (∆S)≥ 0 或的 W ≥ ∆F 不等式,掌管著系統中巧拰i產生的統計分佈和漲落。以正、負總熵產生概率比例表示的漲落定理如下所列:
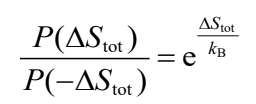
可見總熵產生可以減少,只是其機率在宏觀系統會變得非常非常之小。同時由於概率歸一,可以直接得到積分漲落定理 (Integral FT),同時利用 Schwartz 不等式也直接得到熱力學第二定理了:
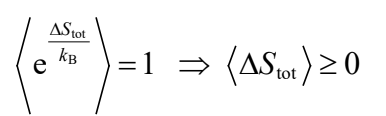
漲落定理最初是由 Evans、Cohen 和 Morriss 在 1993 年發表在《物理評論快報》[3] 上,他們是透過電腦模擬結果而提出漲落定理並進行驗證的。第一個相關的推導是在 1994 年由 Evans 和 Searles 給出的 [4]。自那時起便開啟了統計物理的新時代,其後多年進行了大量的數學和計算工作,以表明漲落定理適用於各種統計系統 (statistical ensemble)。漲落定理對於非平衡統計力學至關重要。其中比較重要的結果是1997年Jarzynski提出的 Jarzynski 等式 [5] 以及 1999年Crooks 提出的 Crooks 定理 [6],近十年更發展到資訊熱力學(Information Thermodynamics)[7]、量子漲落定理 (Quantum FT)[8]、熱力學測不準關係 (Thermodynamics Uncertainty Relation)[9] 及資訊幾何 (Information Geometry)[10] 等領域。漲落定理補救了熱力學第二定律的不足,它包括了傳統的第二定律作為特殊情況。漲落定理很容易就證明第二定律不等式。
簡單來說,漲落定理是描述熵產生分佈對稱性的定律,而熱力學第二定律只是描述這個分佈的平均值恆為非負值。當與中心極限定理 (Central Limit Theorem) 結合時,漲落定理還包含了線性運輸係數的 Green-Kubo 關係。但是漲落定理比Green-Kubo 關係更普適,因為漲落定理適用於遠離平衡的漲落。儘管如此,科學家們仍無法從漲落定理推導非線性響應理論的方程。而Crook's 定理是瞬態漲落定理的一個例子,它把非平衡轉換中的耗散本P自由能差聯繫起來,方便在實驗中驗證漲落定理。
熱力學第二定律只適用於宏觀系統的平均行為,反向的熱力學軌跡仍然有可能出現,並允釵b耗散過程中被觀察到。特別是在自由度少的系統中及在測量時間間隔短時,反向軌跡及其負熵的產生可以在釵h小型系統中,通過軌跡分析被準確的測量到。在理論方面,20多年前開始蓬勃發展的隨機熱力學 (Stochastic Thermodynamics)[11]提供了在介觀尺度下,描述軌跡隨機過程的系統理論計算工具 [11]。這些研究,更加速了非平衡統計物理的迅速發展,近年亦開始進入應用的範疇。
非平衡穩態
細緻平衡 (Detailed Balance, DB) 是平衡統計物理的重要原則,已被用來描述各種物理、化學和生物系統在熱平衡時的動力學。細緻平衡指出當系統平衡時,每個動力學過程應通過其逆過程來保持平衡。細緻平衡的成立條件是系統處於平衡狀態,從而確保每個基本前進過程都 ( 任何過渡時間 ) 由其反向對應項平衡,因此前進和反向躍遷概率比會自動遵循玻爾茲曼分佈。另一方面,非平衡態跟平衡態有很大的不同在於非平衡態經常涉及一個淨通量 ( 質量、動量或熱量 ),使細緻平衡被破壞。實驗上,非平衡狀態可通過施加一種“廣義力”來實現,例如系統溫度或濃度的梯度,速度或化學勢。當廣義力是與時間無關時,系統可以被驅動到非平衡穩態 (Non-equilibrium Steady State, NESS),這也閉O最簡單的非平衡狀態。在非平衡穩態中,平均而言熵以正速率產生,這是不可逆性質具體的度量。儘管人們對平衡時的漲落了解很多,但當前對非平衡態漲落的理解還是相當有限的。對於由大量的粒子組成的非平衡穩態系統,不同粒子軌跡之間的熵產生有很大的漲落。由於粒子身處於複雜的勢能或粒子之間具有的強烈相互作用,這些漲落在空間的不同位置可以有很大差異。
因此便無法把系統視為準平衡 ( 將坐標轉為粒子平均移動速度的參照系 )。同時熵產生量的幅度和其正負值也可有很大的變化,使問題更為複雜。雖然漲落定理預測了正負熵產生概率密度函數比的通用形式為:
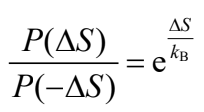
P(ΔS) 函數本身的形式並沒有理論預測或有系統的普遍計算方法。因此,有關的非平衡穩態漲落的更多理解,可以通過檢查粒子軌跡水平上的熵產生和不可逆性來研究。為了更了解非平衡穩態漲落在熵產生中的物理性質,近年來我在多個系統中進行了一些理論和實驗的合作研究,其中最簡單的兩類系統就是 RC 電路系統和單個膠體布朗粒子的直接觀察。
耦合 RC 電路系統
RC 電路是一個方便研究非平衡物理的實驗系統,在恆穩電流驅動下很容易達到方便操控的 NESS 狀態。在熱攪動下其電位差出現所謂的 Johnson-Nyquist 噪聲。而其在電容板上的電荷可對應到布朗運動的粒子位置,且其運動方程往往是線性的,能方便於深入理論並推導出分析解。因此是一個很方便研究布朗運動體系的非平衡物理系統。如圖一 (a) 所示,兩個耦合 RC 電路在各自外電流驅動下或處於不同溫度下都可以達到恆穩的非平衡穩態 [12,13]。中央大學物理系陳永富及李紀倫等人,通過紀錄大量的電位差時間序列數據,得到了相當於布朗粒子的時間軌跡,並據此來測量熵產生及其他非平衡穩態的性質。系統熵的產生可通過時間軌跡之不可逆性或物理過程的耗散兩種方法來計算。實驗數據可以證明兩種方法來計算熵產生的等價性 [13],同時亦直接驗證了 FT( 如圖一 (b) 所示 )。
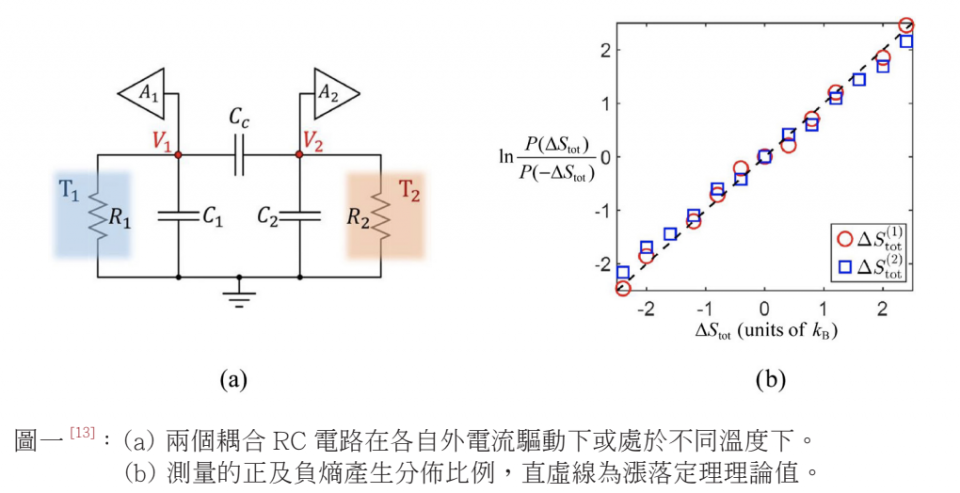
此外,我們在線性耦合 RC 電路系統中,也證明了在兩種不同溫度熱庫的熱力作用下,可以實現自主布朗迴轉器 (Autonomous Brownian Gyrator)[14]。這是由於擴散和驅動之間的不完全抵消而產生機率通量,從而使得系統處於穩定循環定狀態,就像迷你熱機器在機率空間中轉動一樣。
被驅動膠體粒子在周期性勢能上的非平衡穩態
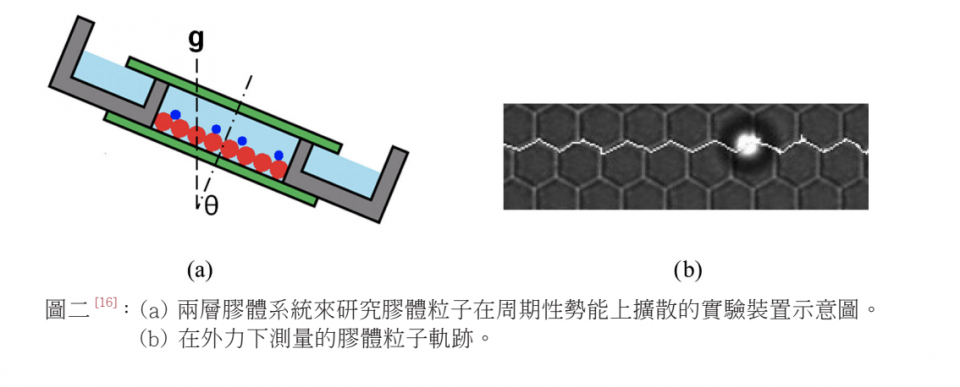
在迄今已探索的非平衡穩態系統中,懸浮在液固界面附近的膠體粒子可以提供一些獨特的研究優勢。因為系統中的粒子移動較慢,可以在單粒子水平上使用視頻顯微鏡術追蹤法。這些典範系統方便用於仔細的研究一系列有趣的相變問題動力學,以及二維軟物質系統。近年來,香港科技大學童彭爾等人,開發了兩層膠體系統來研究膠體在周期性勢能上的擴散 [15]。以膠體球在玻璃基板上形成結晶圖案的底部膠體球提供了週期性的勢能。而膠體晶體的波紋表面層,則提供了頂部粒子擴散的引力勢場 U0。使用光學顯微鏡,可以在熱平衡條件下,測量擴散粒子的統計分佈並通過 Boltzmann 分佈重建了勢場 U0。同時也測量了粒子的動態擴散特性,例如其逃逸時間和擴散係數。兩層膠體系統提供了一個有效的平台來產生外力驅動下的非平衡穩態 ( 見圖二 (a)),並能夠從單粒子層次去同時追蹤多個粒子的軌跡運動以及測量外部勢能。這樣的方法可以用於研究一系列非平衡統計物理學中有趣的問題。例如,當整個樣本以角度 θ 相對於垂直重力方向傾斜時,引力的切線分力 F 會施加到頂層的擴散顆粒。在這種情況下,由於存在穩定的粒子通量,並且系統被驅動進入非平衡穩態,可方便仔細地測量大量數據。在最近的實驗 [15,16] 中,我們測量了粒子的平均漂移速度 ν(F, Eb) 和擴散係數 D(F, Eb) 作為 F 的函數 ( 通過改變傾斜角 θ ) 和勢壘高度 Eb( 通過使用不同的膠體樣本 )。測得之 ν(F, Eb)和 D(F, Eb) 的結果,非常吻合一維漂移速度和擴散係數 [16]。
此外,對於傾斜的周期勢,我們測量了非平衡穩態概率密度函數PSS。PSS 偏離平衡的波茲曼分佈之程度取決於驅動力或與平衡態之間的距離。同時也首次由理論推算出一般一維週期勢能下之非平衡穩態密度函數分佈的精確公式 [16,17]:
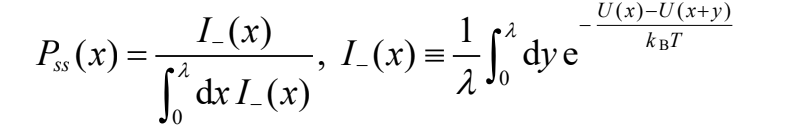
其中 U(x) 為週期 λ 的任意函數: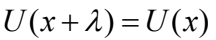 。此理論結果亦經由上述膠體擴散實驗獲得精確的驗證 [17,18]。
操控非平衡猶似平衡:布朗粒子的等溫捷徑 。此理論結果亦經由上述膠體擴散實驗獲得精確的驗證 [17,18]。
操控非平衡猶似平衡:布朗粒子的等溫捷徑
由於非平衡統計力學近年的進展與尖端實驗技術的掌握,現時我們已開始邁進應用在非平衡控制及操控微型熱力學系統了。其中最基礎就是如何有效去操控各種熱力學過程。而這些熱力學過程,如等溫、絕熱過程等等,是建構熱機器的重要基本步驟。等溫過程(Isothermal process) 是經典熱力學中的基石,從一個平衡狀態到另一個平衡狀態的過渡要在準靜態 (quasi-static) 下進行,也就是需要很長時間才能完成。得益於操縱奈米物體的最新技術進步,例如光學鑷子、磁性鑷子和反布朗電運動 (Anti-Brownian Electrokinetic) 陷阱,人們將更多的精力集中在了解熱漲落主宰的微米系統上。特別是,布朗熱機 (Brownian Engine) 的實現使得科學家們將注意力重新集中在隨機熱力學中的熱力學過程上。
其中一個重要的問題是 : 是否有可能以比固有弛豫時間短得多的時間,將系統從一個平衡態加速到另一個平衡態,從而獲得與準靜態過程相同的行為性質。
在過去的十年中對量子系統及隨機環境中進行了釵h研究,這些方法被稱為絕熱捷徑。這些捷徑需要額外的能量來抑制高度的非平衡漲落。最近由北京師範大學珖i春等人提出的等溫捷徑 (Shortcuts-to-Isothermality, ScI) 方法 [19],提供了一個統一的理論框架。為了使系統的演化始終與外加勢能保持瞬時平衡,需要引入對應輔助勢以實現有限速率的等溫過程,並確定非平衡過程中作奶岔鰜Y。然而這些提出的加速捷徑方法尚未在實驗中確立,尤其是探索這種快速等溫轉變所需的熱力學成本。加速等溫過程對於實現微型熱力發動機的熱力學循環具有根本和現實的重要性,而等溫捷徑可以顯著加快發動機循環速度。在實驗中了解等溫捷徑流程的相關成本,對於提高此類微引擎的設計效率至關重要。
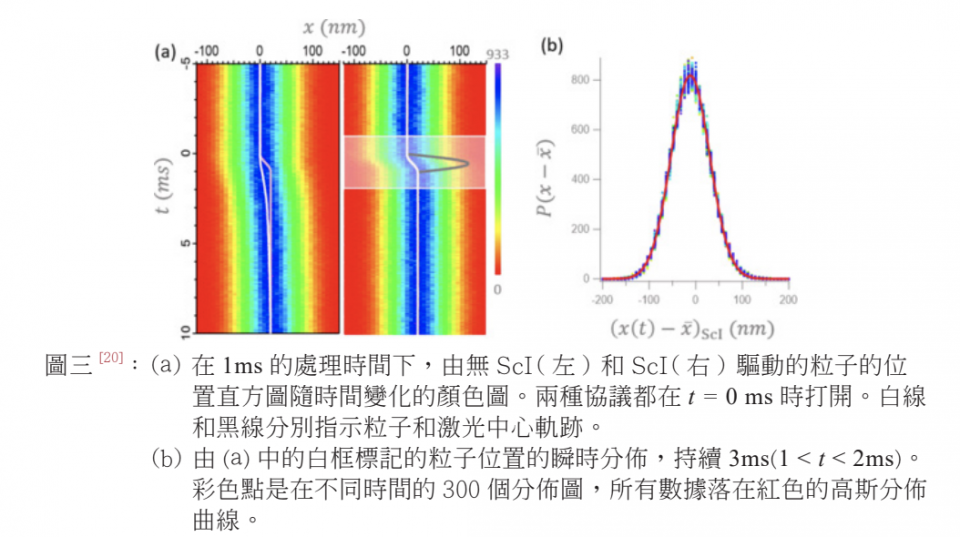
最近中央大學物理系田溶根等人,在布朗粒子系統中實現了等溫捷徑及測量了過程所需的熱力學能量成本 [20]。該過程可以在有限的時間加速等溫過程。實驗使用一個布朗粒子,該粒子在有限時間內快速被簡諧勢 (harmonic potential) 拖行在兩個不同平衡態位置。我們在理論上和實驗上都確認,在這些等溫捷徑過程中,位置滿足波茲曼分佈 ( 如圖三所示 )。這過程中左熒妓v分佈函數是高斯的。並且等溫捷徑過程的耗散本P行駛時間成反比,這表明由於行駛成本的增
加,不可能無限迅速地進行過渡。
在另一方面,熱機 (Heat engine) 是熱力學的基礎,並已經在釵h領域中被進行了研究。經由回饋技術的進步和操縱小物體技術的掌握,在過去的十年中,人們對微觀熱機已經在隨機系統中有了一些認識。通過光鑷 (Optical Tweezers, OT) 所產生的簡諧勢的彈簧常數進行控制,從而對布朗粒子施行等溫壓縮和膨脹過程,繼而能夠在真正的溫度下實現了斯特林發動機循環 (Stirling engine cycle)。要使到熱機可以達到效率的熱力學之極限,準靜態過程是必要的。在這裡,出現了一個基本而重要的問題:是否可能使熱機在有限的循環時間內達到極限效率?實現它的一種方法是建立一個可以在有限時間內加速的發動機循環,但仍然可以再現與準靜態過程相同的輸出。利用上述快速等溫壓縮過程中,布朗粒子的平衡和以有限速率膨脹之等溫捷徑 (ScI),我們期望能夠實現以有限速率在過渡期間,維持瞬時平衡的等溫過程。等溫捷徑在移動簡諧勢中的傳輸,使用了光鑷進行實驗證明。但另一方面,有限速率等溫膨漲,由於簡諧勢所需的彈簧常數為負 ( 即排斥力 ),這是傳統光鑷無法實現的彈簧常數,因此是一個尚未解決的難題。田溶根等人實現了一個簡單解決方案 [21]:使用光反饋阱 (Optical Feedback Trap)[22] 通過創建跟時間有關的簡諧勢,以提供等溫膨漲所需的負彈簧常數。利用此方法同時亦證明了負常數的簡諧勢足以推動粒子,並可以實現等溫捷徑膨脹。此外,更驗證了諸如�,熱和內能之類的熱力學量確實滿足隨機熱力學之預測。
參考文獻:
[1] "Fluctuation relations: a pedagogical overview", Richard Spinney and Ian Ford, Chapter 1 in Nonequilibrium Statistical Physics of Small Systems: Fluctuation Relations and Beyond , edited by R. Klages, W. Just and C.Jarzynski (Wiley-VCH, Weinheim 2013). https://onlinelibrary.wiley.com/doi/pdf/10.1002/9783527658701
[2] "Boltzmann's H theorem and the Loschmidt and the Zermelo paradoxes", Ta-You Wu, International J. of Theo. Phys. 14, 289 (1975).
[3] "Probability of second law violations in shearing steady states", D. J. Evans ,E.G.D. Cohen and G.P. Morriss, Phy. Rev. Lett. 71, 2401 (1993).
[4] "Equilibrium microstates which generate second law violating steady states",D. J. Evans and D. J. Searles, Phys. Rev. E 50, 1645 (1994).
[5] "Nonequilibrium equality for free energy differences", C. Jarzynski, Phys. Rev.Lett., 78, 2690 (1997).
[6] "Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences", G. Crooks, Phys. Rev. E 60, 2721 (1999).
[7] "Generalized Jarzynski Equality under Nonequilibrium Feedback Control", T. Sagawa and M. Ueda, Phys. Rev. Lett. 104, 090602 (2010).
[8] "Colloquium: Quantum Fluctuation Relations: Foundations and Applications", M. Campisi, P. Hänggi, and P. Talkner, Rev. Mod. Phys. 83, 771 (2011).
[9] "Thermodynamic uncertainty relation for biomolecular processes", A. C. Barato and U. Seifert, Phys. Rev. Lett. 114, 158101 (2015).
[10] "Stochastic Thermodynamic Interpretation of Information Geometry", S. Ito, Phys. Rev. Lett. 121, 030605 (2018).
[11] Stochastic Energetics, K. Sekimoto (Springer, Berlin 2010).
[12] "Fluctuations of entropy production in partially masked electric circuits", K.- H. Chiang, C.W. Chou, C. L. Lee, Pik-Yin Lai, and Y. F. Chen, Europhys. Lett. 113, 30001 (2016).
[13] "Entropy production and irreversibility of dissipative trajectories in electric circuits", K. H. Chiang, C. L. Lee, Pik-Yin Lai, and Y. F. Chen, Phys. Rev. E 95, 012158 (2017).
[14] "Electrical Autonomous Brownian Gyrator", K.-H. Chiang, C.W. Chou, C. L. Lee, Pik-Yin Lai, and Y. F. Chen, Phys. Rev. E 96, 032123 (2017).
[15] "Colloidal diffusion in a periodic energy landscape", X. G. Ma, Pik-Yin Lai, and P. Tong, Soft Matter 9, 8826 (2013).
[16] "Colloidal transport and diffusion over a tilted periodic energy potential: dynamics of individual particles ", X. G. Ma, Pik-Yin Lai, B. Ackerson, and P.Tong, Soft Matter 11, 1182 (2015).
[17] "Colloidal Dynamics over a tilted periodic energy potential: non-equilibrium steady-state distributions ", X. G. Ma, Pik-Yin Lai, B. Ackerson, and P. Tong, Phys. Rev. E 91, 042306 (2015).
[18] "Colloidal Dynamics over a tilted periodic energy potential: Forward and reverse transition probabilities and Entropy production in non-equilibrium steady-state", X. G. Ma, Y. Su, Pik-Yin Lai, and P. Tong, Phys. Rev. E 96,012601 (2017).
[19] "Shortcuts to isothermality and nonequilibrium work relations", G. Li, H. T. Quan, and Z. C. Tu, , Phys. Rev. E 96, 012144 (2017).
[20] "Thermodynamic cost of shortcuts-to-isothermal transport of a Brownian particle ", J. A. C. Albay, S. R. Wulaningrum, C. Kwon, Pik-Yin Lai, and Yonggun Jun, Phys. Rev. Res . 1, 033122-1~8 (2019).
[21] "Realization of finite-rate isothermal compression and expansion using optical feedback trap", J. A. C. Albay, Pik-Yin Lai, and Yonggun Jun, App. Phys. Lett. 116, 103706 (2020).
[22] "Optical tweezers as a mathematically driven spatio-temporal potential generator", J. A. C. Albay, G. Paneru, H. K. Pak, and Yonggun Jun, Optics Express, 26, 29906 (2018).
|
|

